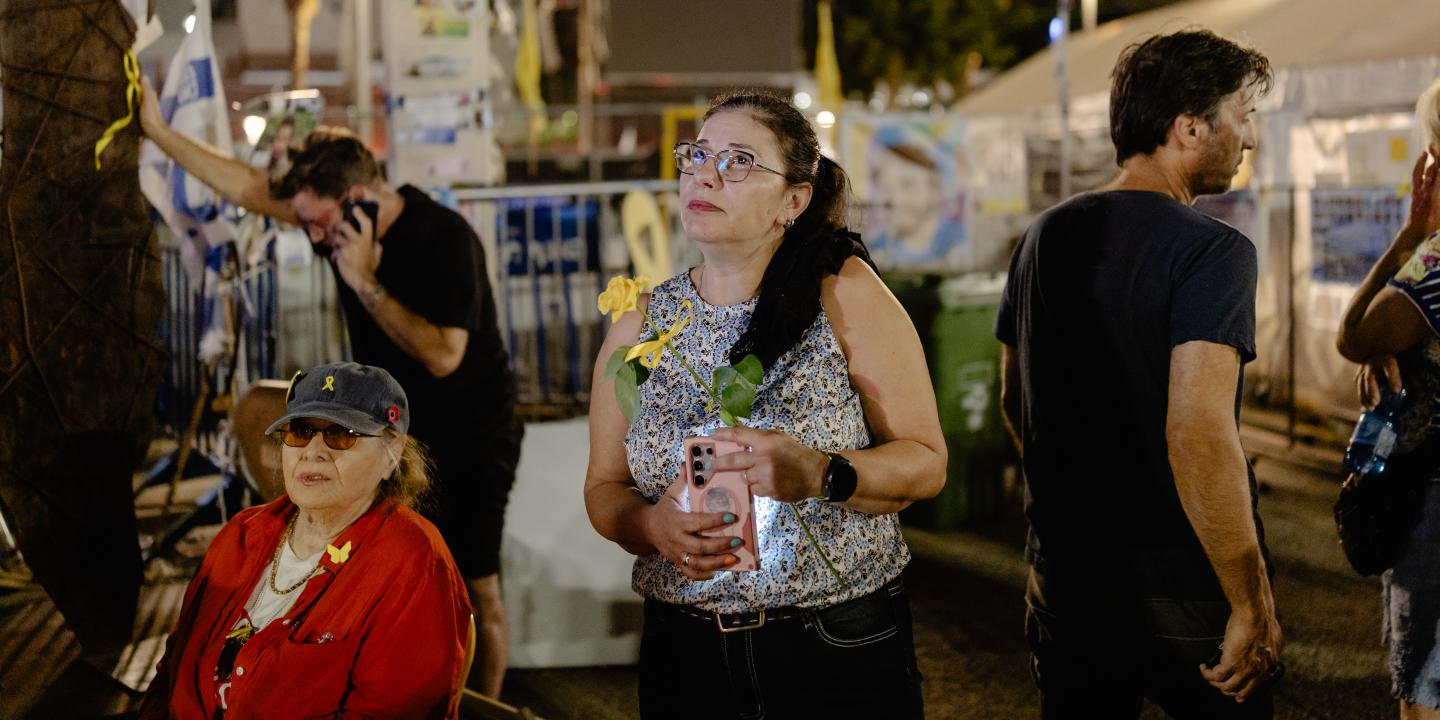Français
English
Deutsch
Italiano
Русский
Español
Nicolas de Condorcet (1743-1794) fut l’un des premiers à se pencher sérieusement sur une question qui traverse l’histoire parlementaire : combien de députés faut-il pour bien représenter un pays ? La difficulté est toujours la même : une assemblée ne doit être ni trop nombreuse, au risque de devenir lente, confuse et sujette aux passions, ni trop réduite, sous peine de ne plus refléter la diversité des opinions et des intérêts. Dans ses projets constitutionnels (notamment celui de 1793), le mathématicien et philosophe plaide pour une approche rationnelle fondée sur des arguments mathématiques : selon lui, le nombre de députés doit s’adapter à la population, sans jamais affaiblir l’efficacité des débats et des décisions.
Ce raisonnement, très moderne pour l’époque, repose sur une idée simple. Chaque député représente un certain nombre de citoyens, mais il doit aussi discuter, négocier et collaborer avec ses collègues. La qualité d’un parlement dépend autant de sa représentativité que de sa capacité à travailler efficacement. Si l’une de ces dimensions prend trop de poids, l’équilibre se rompt. Condorcet en conclut que le nombre d’élus « optimal » croît avec la population, mais moins vite qu’elle. Deux siècles plus tard, cette intuition a trouvé une confirmation quantitative. Dans les années 1950, les politistes ont montré que, dans la plupart des démocraties, le nombre de parlementaires suit une régularité étonnante : il est de l’ordre de la racine cubique de la population.
Voici l’idée générale, un peu technique sans doute, mais que le lecteur pourra passer sans dommage. Supposons une population totale P représentée par D députés. Chacun représente en moyenne P/D citoyens. Mais les députés doivent aussi débattre entre eux : chacun échange avec tous les autres, ce qui représente, au total, environ D2 relations internes. Si l’on considère que ces deux missions – représentation et délibération – doivent avoir un poids comparable, on peut écrire que P/D doit être comparable à D². Autrement dit, le nombre de députés « optimal » devrait croître approximativement comme la racine cubique de la population.
Il vous reste 43.3% de cet article à lire. La suite est réservée aux abonnés.
